Гурток: «Фізика»
Гурток: «Фізика»
Керівник гуртка: Лимар Валентин Іванович
Електрона пошта: mfe2020@ukr.net
Задача «Парадокс кінетичної енергії» (експеримент з іграшковим автомобілем) [Е.И. Бутиков, А.А. Быков, А.С. Кондратьев «Физика в примерах и задачах». – М., СПб.: МЦНМО, Петроглиф, 2015. – 516 с.]
Іграшковий автомобіль із повністю заведеною пружиною набуває швидкості v. Нехтуючи втратами енергії на тертя, можемо вважати, що потенціальна енергія заведеної пружини W повністю перетворюється у кінетичну енергію руху іграшки. Але розглянемо цей процес в іншій системі відліку, яка рухається зі швидкістю v відносно Землі назустріч іграшковому автомобілю. У цій системі відліку набута швидкість іграшки дорівнює, очевидно, 2v, тобто у два рази більше, а її кінетична енергія у чотири рази більша, тобто дорівнює 4W. Так як у цій системі відліку автомобіль від самого початку мав кінетичну енергію W, то в результаті розкручування пружини кінетична енергія іграшки збільшилася на 3W, а не на W, як у вихідній початковій системі відліку. Між тим потенціальна енергія заведеної пружини в обох системах відліку дорівнює W !!! Поясніть описаний парадокс, адже, на перший погляд, здається, що закон збереження енергії не виконується у рухомій системі відліку (при фундаментальному положенні про рівноправність у фізиці усіх інерціальних систем відліку).
https://www.youtube.com/watch?v=roFrbTwvKxg&list=PLM7EiFMa0zoUkVmDP1E6dg8hsdk6Z7tOe&index=261
https://www.youtube.com/watch?v=AlaBXFtZ8kA
https://www.youtube.com/watch?v=QsyZuhTO0Uk&t=9s
Задача «Лабораторна модель петлі Нестерова» [Е.И. Бутиков, А.А. Быков, А.С. Кондратьев «Физика в примерах и задачах». – М., СПб.: МЦНМО, Петроглиф, 2015. – 516 с.]
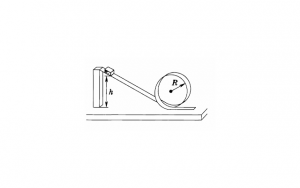
І рівень. Невелике тіло зісковзує без тертя по похилому жолобі, який потім переходить у кругову «мертву петлю» радіусом R. З якої мінімальної висоти h потрібно відпускати тіло без початкової швидкості, щоб воно не відірвалось від жолоба (подолало «мертву петлю»)? (Рис. 1).
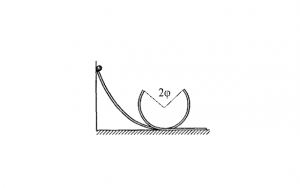
ІІ рівень. Якою має бути початкова висота для того, щоб тіло змогло подолати «мертву петлю» з симетрично вирізаною верхньою частиною (відео 3), кутовий розмір вирізу дорівнює 2φ ? (Рис. 2).
ІІІ рівень. Провести рішення задачі, якщо замість тіла, що зісковзує, маємо кульку, яка скочується (так, як показано на усіх трьох запропонованих відео).
Це цікаво!
https://www.youtube.com/watch?v=OPlS3LYcUoM
https://www.youtube.com/watch?v=XMvDSu05xiM
https://www.youtube.com/watch?v=YzXM0cGBgLA&list=PLM7EiFMa0zoUkVmDP1E6dg8hsdk6Z7tOe&index=199
Задача «Про поєднані мильні бульбашки» ( Гнэдиг П., Хоньек Д., Райли К., «Двести интригующих физических задач» – М.: Бюро Квантум, Техносфера, 2005. – 272 с.).
Дві мильні бульбашки радіусами R1 та R2 з’єднані тонкою скляною трубкою. Повітря переходить з однієї бульбашки до іншої, і, як результат, утворюється тільки одна бульбашка радіусом R3. I рівень. Визначити коефіцієнт поверхневого натягу мильної плівки, якщо тиск навколишньої атмосфери дорівнює p0. IІ рівень. Наскільки надійним є запропонований метод визначення коефіцієнта поверхневого натягу мильної плівки? ІІІ рівень. Які обставини загальнофізичного змісту визначають «напрям» перетікання повітря від однієї бульбашки до іншої?
https://www.youtube.com/watch?v=5gTXd-uddQE&list=PLM7EiFMa0zoUkVmDP1E6dg8hsdk6Z7tOe&index=2
Задача «Про ізохронні гармонічні коливання» Х. Гюйгенса. На запропонованому відео ведучий В.І. Гервідс вказує на необхідні умови для отримання гармонічних коливань кульки у «потенціальній ямі». I рівень. Як вказані необхідні умови пов’язані із законом збереження енергії? ІІ-ІІІ рівень. Якою при цьому має бути траєкторія руху кульки (і, відповідно, форма вигину направляючих, по яких кулька рухається)? Поясніть у звязку з цим, на якісному рівні, принцип побудови Х. Гюйгенсом «ізохронного» математичного маятника.